Une maladie touche une personne sur mille. On dispose d’un test la détectant avec une fiabilité de 99 % et donnant de fausses alertes dans 5 % des cas. Mon test est positif, suis-je condamné ?
La réponse :
A première vue, on pourrait penser qu’un test avec une fiabilité de 99% et un taux de 5% de fausses alertes est un test assez fiable et que la probabilité que nous soyons malade est forte. Il n’en est rien !
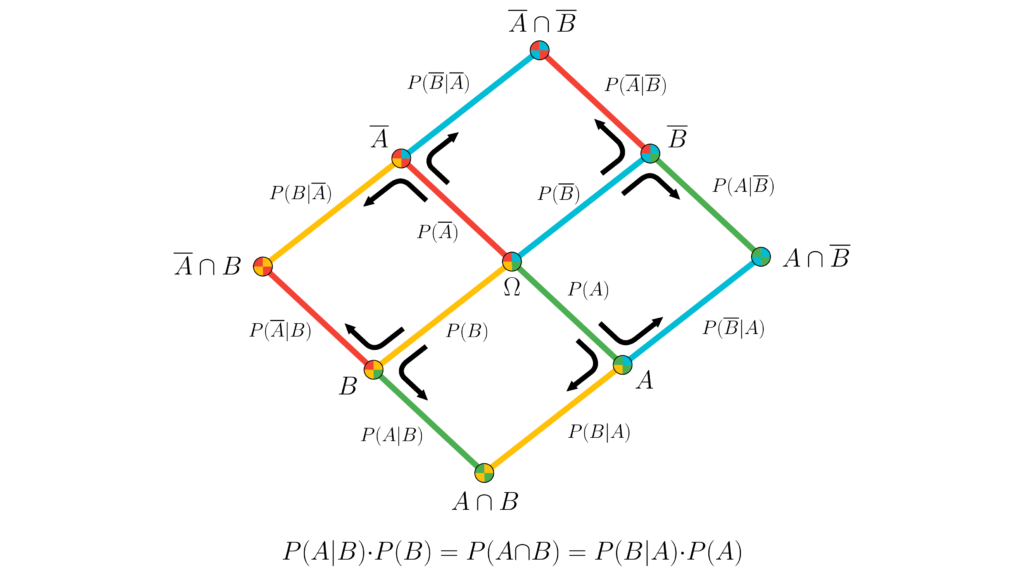
Ici, ce que l’on cherche à estimer est la probabilité d’être malade sachant qu’un test nous déclare positif. Cette probabilité, notée P(Maladie | Positif), peut s’obtenir en fait par le Théorème de Bayes, l’un des principaux théorèmes de la théorie des probabilités, qui permet de déterminer la probabilité qu’un événement arrive à partir d’un autre évènement qui s’est réalisé, notamment quand ces deux évènements sont interdépendants :
P(Maladie | Positif) = (P(Positif | Maladie) x P(Maladie)) / P(Positif)
Ce qui, d’après les probabilités de l’énoncé, donne :
P(Maladie | Positif) = ( 0,99 x 0,001 ) / ( 0,99 x 0,001 + 0,05 x 0,999) = 0,0194
On en conclut donc qu’on a environ 1,94% de chance d’être vraiment malade lorsque l’on reçoit un résultat positif au test. Ce résultat est très contre-intuitif, mais il prend pourtant tout son sens lorsqu’on l’aborde avec de bonnes connaissances en statistiques et probabilités !
Pour développer le sujet de ces fondamentaux, vous pouvez suivre nos formations. Consultez notre catalogue complet ou contactez-nous directement.
