ENJEUX
Dans l’objectif d’évaluer la tenue des cuves des réacteurs du parc nucléaire français sous chargement thermomécanique en fonction de la durée d’exploitation, l’Institut de Radioprotection et de Sûreté Nucléaire (IRSN) développe ses propres outils d’analyse et de vérification lui permettant entre autres de pouvoir se positionner vis-à-vis des résultats des exploitants. Dans ce sens, l’IRSN a développé une chaine de calcul déterministe permettant d’évaluer la tenue de la cuve en présence d’un défaut donné et sous un chargement thermomécanique donné.
L’IRSN a fait appel à Phimeca afin de développer des scripts de couplage mécano-probabiliste (langage python – bibliothèques OpenTURNS) permettant le calcul de la probabilité de la rupture d’une cuve soumise à des chargements thermomécaniques donnés en présence d’incertitudes matérielles et géométriques de types aléatoire et épistémique.
Méthodologie et principales réalisations
Phimeca a construit plusieurs scripts python qui assurent les fonctionnalités suivantes :
- Réalisation d’un couplage mécano-probabiliste entre Python et le code Cast3m.
- Définition d’un modèle probabiliste des paramètres d’entrées du modèle Physique avec plusieurs configurations des distributions : Déterministe, Uniforme, Bernoulli, Normale,Log-Normale ou définie par un tableau de probabilité fourni par l’utilisateur.
- Réalisation de calcul de probabilité de défaillance du système (Pf_sys) avec les méthodes de Monte-Carlo et de Subset.
- Réalisation de calcul de fragilité de Pf_sys en fonction d’un ou de plusieurs indicateurs.
- Réalisation d’un calcul inverse,en cherchant les valeurs de plusieurs indicateurs qui correspondent à un seuil de probabilité de défaillance donné.
- Représentation graphique des résultats de calcul de fragilité et de calcul inverse.
En résumé, ces scripts Python constituent un outil puissant pour analyser la fiabilité des systèmes complexes en prenant en compte l’incertitude des paramètres d’entrée et pour optimiser leur conception afin de répondre à des critères de fiabilité spécifiques.
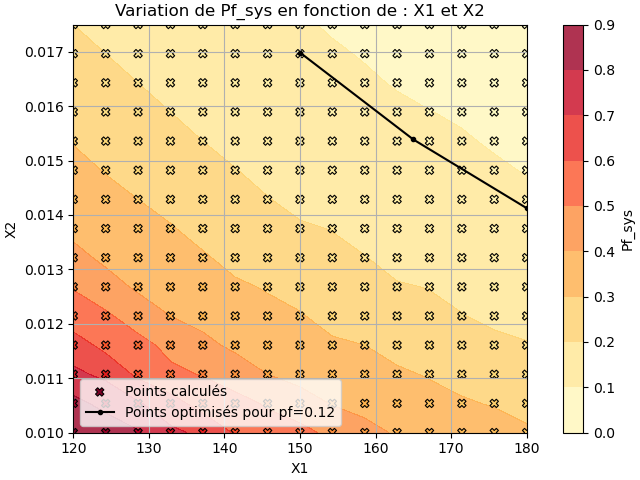
Figure 1: Résultat fictif et illustratif d’un type de résultat attendu pour un modèle sinusoïdal
